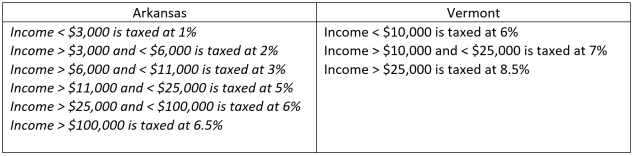One of the stated goals of the Pillar One Blueprint (Pillar One) and the Pillar Two Blueprint (Pillar Two) is the desire of the OECD/Inclusive Framework (OECD/IF) to reduce tax complexity for both taxpayers and tax jurisdictions. Tax complexity imposes compliance costs and distorts behaviors, making the principles of a good tax system harder to achieve. Given that reducing tax complexity is an important goal for both Blueprints, a relevant question that we address is: How complex are the Blueprints?
This article assesses the Blueprints in terms of one particular type of tax complexity: rule complexity, i.e., the problems faced by taxpayers when interpreting the written and unwritten tax rules (Bradford 1986, cited below). Rule complexity is generated when government documents (e.g., regulations, guidelines, manuals) are extensive and detailed, or have many interrelated and interdependent parts that overlap or interact with one another. As a result, tax laws are difficult to understand, and legal problems are difficult to solve. Thus, rule complexity has a detrimental impact on day-to-day tax compliance work for the taxpayer.
We build on the literature on the complexity of algorithms and software—in particular on Halstead’s measures for software complexity (Maurice H. Halstead. Elements of Software Science (Operating and Programming Systems Series), 1977, Elsevier) The Halstead measures have recently been used by Jean-Edouard Colliard and Co-Pierre Georg in Measuring Regulatory Complexity to assess the complexity of bank regulations. The key to our approach is to classify words in normative texts as operators and operands. Operators in an algorithm are symbols such as +, -, =, “if,” and “else” indicating that an operation has to be performed. Operands in an algorithm are variables and values that serve as inputs and outputs in the different operations. We provide our dictionary of classified words online at Github. An Appendix, which explains the rules we followed to classify words into these three categories and provides a number of examples, is attached to the TMIJ version of this article.
The tax complexity of one document (e.g., regulations, manuals, guidelines) is meaningful only when measured in a relative sense, either by comparison with another document or by examining changes in one document over time. For comparison purposes we therefore use the 2017 OECD Transfer Pricing Guidelines (“TPG” or “OECD Guidelines”) and the 2017 United Nations (UN) Practical Manual on Transfer Pricing for Developing Countries (“TPM” or “UN Manual”). In sum, our goal is to compare the tax complexity of four sets of international transfer pricing documents—the TPG, TPM, Pillar One, and Pillar Two—and answer the question: Do Pillar One and Pillar Two exhibit more or less tax complexity when compared with the TPG and TPM? (It is worth noting that the Blueprints are negotiating drafts with many unresolved issues whereas the TPG and TPM are finalized documents; this difference might affect their tax complexity metrics.)
We start by defining tax complexity and providing a brief overview of the literature on this topic. We then explain our tax complexity measures and use them to assess the relative complexity of the four documents. We find that the ranking (from highest to lowest tax complexity) is Pillar One > Pillar Two > TPM > TPG. We conclude with some overall policy recommendations for reducing tax complexity.
DEFINING TAX COMPLEXITY
Nearly 250 years ago, Adam Smith in Book V, Chapter 2 of An Inquiry into the Nature and Causes of the Wealth of Nations outlined four maxims for a good tax system: tax payments should be equal, certain, convenient, and economical for all taxpayers. Smith’s maxims III and IV, convenience and economy, merged over time into what economists now refer to as tax simplicity or as its inverse or antonym, tax complexity. (Tax payments were to be “as convenient to the contributor, both in the time and in the mode of payment, and, in proportion to the revenue which they brought to the prince, as little burdensome to the people.” It is also interesting to note that Smith ranked tax certainty (i.e., that taxes should be “clear and plain”) as more important than equality of tax payments.)
Because tax complexity has exactly the reverse effects to Smith’s third and fourth maxims—raising administration, compliance, and enforcement costs rather than being convenient and economical—reducing tax complexity has long been viewed as an important goal for tax authorities. The Blueprints are no exception; tax complexity is mentioned, by our count, 364 times in the two documents. Tax complexity is mentioned 172 times in Pillar One and 192 times in Pillar Two. (We searched using the words administrative burden, complexity, compliance, simplicity, and simplification. The Blueprints state over and over again that reducing tax complexity is a major goal of this process.)
Our goal in this article is to assess the tax complexity of the Blueprints. Tax complexity is easy to recognize but harder to define because it is multi-faceted. Of the various definitions perhaps the best known is the definition in David Bradford’s book Untangling the Income Tax (Cambridge, Mass.: Harvard Univ. Press 1986; pp. 266–267). Bradford decomposes tax complexity into three components: (1) rule complexity (problems faced by taxpayers when interpreting the written and unwritten tax rules); (2) compliance complexity (the problems of keeping records, choosing forms, making calculations, etc.); and (3) transactional complexity (problems faced by taxpayers engaged in tax planning; i.e., arranging their affairs so as to minimize taxes within the framework of the rules).
A SIMPLE EXAMPLE OF TAX COMPLEXITY
Of Bradford’s three components of tax complexity, the measure we focus on is rule complexity, i.e., the problems faced by taxpayers when interpreting the written and unwritten tax rules. While some measures of tax complexity are designed to capture the complexity of an entire tax system (i.e., not only the legal documents but how the texts are implemented in practice), rule complexity focuses on the complexity of documents. Our approach builds on Colliard and Georg’s (2020) paper on the complexity of banking regulation and applies similar ideas in the context of tax law. The main idea is that some legal texts, in particular tax law, can be seen as a set of rules that determine for a given input (the characteristics of the taxpayer) a unique output (the amount of tax to be paid). In other words, tax law can be interpreted as an algorithm. Computer scientists have proposed a number of measures of algorithmic complexity, which we can use to assess tax complexity.
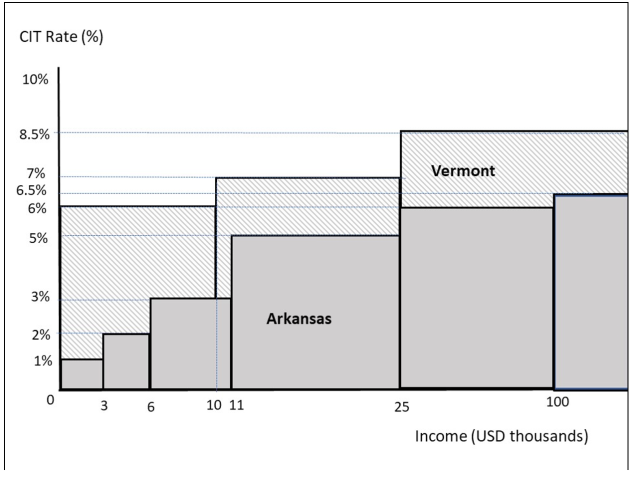
To illustrate the analogy and introduce some definitions, we start with a simple example comparing the tax complexity of the computation of the state corporate income tax (CIT) in Arkansas and Vermont for 2020. Table 1(a) summarizes the tax rates and brackets for the two states; Table 1(b) reports on our measures of their tax complexity. Figure 1 illustrates the two CIT rules.
Table 1(a): State CIT Rates in Arkansas and Vermont
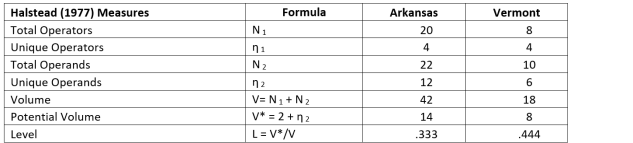
Table 1(b): Halstead Rule Complexity Measures
Figure 1: State Corporate Income Tax Rates in Arkansas and Vermont, 2020
Based on the data in Table 1(a), intuitively it looks like the CIT rules in Arkansas are more complex since they take twice as many lines of text, but can we give a precise assessment of their tax complexity? Can we quantify their complexity? For instance, Arkansas uses six different income brackets, while Vermont uses three. Does that mean that the rules in Arkansas are twice as complex?
The earliest measures of complexity that were proposed in computer science are the so-called “Halstead measures.” Halstead’s idea was to measure the “psychological complexity” of an algorithm, that is, how difficult it is for a human to understand the operations performed by the algorithm. In computer science, this is typically related to the probability that the algorithm suffers from coding mistakes.
Our first step, following Halstead, is to classify the symbols in the algorithm into operators and operands, where operators are symbols such as +, -, =, “if,” and “else” indicating that an operation has to be performed; and operands are variables and values serving as inputs and outputs in the different operations. Applying these definitions to the rules in Table 1(a), we find:
- Operators: <, >, “is taxed at“
- Operands: income, 3,000, 6,000, 10,000, 11,000, 25,000, 100,000, 1%, 2%, 3%, 5%, 6%, 6.5%, 7%, 8.5%
We now treat the two state CIT rate schedules as separate documents. Using Halstead’s notations, we denote N1 and N2 as the total number of operators and operands, and η1 and η2 as the number of unique operators and operands, respectively. Our results, reported in Table 1(b), are:
- Arkansas: N1 = 20, N2 = 22, η1 = 4, and η2 = 12
- Vermont: N1 = 8, N2 = 10, η1 = 4, and η2 = 6
These numbers capture different dimensions of tax complexity. Note first that η1, the number of unique operators, is the same (4) in both states. The number of unique operands, η2, on the other hand, is twice as high in Arkansas as in Vermont (12 vs. 6) because there are twice as many tax brackets. Thus, a tax professional needs to conduct the same number of distinct operations, but with double the tax brackets; in effect, the diversity of unique operands is twice as high as for unique operators in Arkansas compared with Vermont.
Halstead also included each tax rule’s length, or volume (V), measured as N1 + N2, the total number of operands and operators. In our example, V = N1 + N2 = 42 for Arkansas, and V = 18 for Vermont, so the volume is higher also for the CIT in Arkansas than in Vermont. On this dimension also, the Arkansas tax rule is more complex than in Vermont.
Intuitively, however, there is more to complexity than the mere volume of a document as measured by its total number of operators and operands. Even though the volume for Arkansas is more than double that for Vermont, most people would probably agree that the complexity is not that much higher. (Moreover, from the taxpayer’s perspective, the additional complexity is likely offset by the lower rates for the different income brackets.) A key insight from Halstead is that the complexity of a rule is not only reflected by its length but also to the number of distinct operands used for a given length. Intuitively, a long document using few distinct operands is probably giving detailed explanations on the operations to be performed and may be perceived as less complex than a shorter but less transparent document.
To address this issue, Halstead proposed two measures to control for the different lengths of different algorithms. The first was potential volume, denoted V*. The idea of potential volume is that there are many ways to write the rules for computing the tax rate in Vermont. However, any rule that implements the desired tax rate in Vermont must at least contain the six unique operands (income, 10,000, 25,000, 6%, 7%, 8.5%), the “is taxed at” operator, and at least one other operator. Thus, the shortest possible volume, or “potential volume” of this rule is V* = 2 + η2 = 8. For Arkansas, V* is 14. (See Table 1(b).) The higher potential volume in Arkansas is generated by the inputs of the CIT rules in Arkansas being more numerous than in Vermont, and this would be true for any text describing these tax rules. V* can therefore be conceptualized as the necessary or minimum level of complexity for a document; if the tax rules demand that these parameters must occur in the computation, it is impossible to have a shorter text.
As a second measure, Halstead proposed the level, denoted L, of tax complexity. The idea of level is that an algorithm that is close to the shortest possible algorithm must use a very specialized language and therefore will likely be very difficult to understand. Conversely, if the algorithm is longer but implements the same rules, it is probably introducing more intermediary steps in the computation and should be easier to follow. The level is defined simply as the ratio of potential volume to total volume; that is, L = V*/V. In our example, the level is 14/42 = 0.333 for Arkansas, and 8/18 = 0.444 for Vermont. This means that the level is one-third higher for the Vermont CIT rules than for Arkansas.
The three measures V, V*, and L each capture different characteristics of rule complexity based on the actual and potential volume of operators and operands in a text. Intuitively, the greater the overall length or magnitude of the tax rule, the more difficult it is to understand and follow. While the Arkansas rules are clearly more complex than the Vermont rules, considering the difference in level (V*/V) explains why they are not twice as complex as a comparison based solely on volume would suggest.
This simple example comparing CIT rates in two U.S. states illustrates the different Halstead measures of rule complexity. The number of unique operators η1 captures how many different operations are necessary to compute the tax amount. The number of unique operands η2 captures the number of distinct concepts that must be understood. The volume V simply measures the total number of operators and operands. Potential volume V* captures the minimum number of unique operands (plus 2) needed to explain a tax rule. The Arkansas CIT uses more different parameters and is thus has a higher V*. The level L captures the fact that the Arkansas tax rules always repeat the same structure (an income bracket and a tax rate); thus, while both V* and V are higher in Arkansas than in Vermont, their ratio L = V*/V is lower in Arkansas. The complexity level is therefore lower in Arkansas than in Vermont on this Halstead dimension.
COMPARING THE TAX COMPLEXITY OF FOUR TRANSFER PRICING TEXTS
Applying Halstead’s Measures
We now apply these measures to the four texts: the OECD Guidelines, UN Manual, Pillar One, and Pillar Two. To make the texts more comparable, we remove the Glossary sections from the documents. For the UN Manual, we also report our measures of tax complexity both including and excluding “Part D, Country Practices,” which contains country chapters for Brazil, China, India, Mexico, and South Africa.
Coding tax rules as an algorithm, following along the lines we used above with the Arkansas and Vermont taxes, is time consuming and not readily doable for legal documents that are hundreds of pages long. As a result, we need to directly work on the original text rather than translate it into code. We believe the distinction between operands and operators still applies in a text and the Halstead measures can be directly computed. The key is to classify the words in each of the documents into three categories: operands, operators, and others. Operands are words or expressions that, if the text were translated into an algorithm, would be variables or numbers. Operators are words or expressions that would be translated into mathematical or logical operations. Others are those that would not be translated, typically words that are necessary for grammatical reasons.
To build the classification we need, we start with the dictionary in Colliard and Georg (2020), which the authors built by manually classifying the words in the Dodd-Frank Act. We add the terms contained in several transfer pricing glossaries. Finally, we manually classify the remaining words in the sections relevant to profit splits in the TPG, TPM, and Pillar One. We obtain a dictionary of nearly 10,000 words that we make available online. We believe that our dictionary captures a significant share of the operators and operands in most transfer pricing regulations, allowing interested researchers to repeat our analysis on other documents.
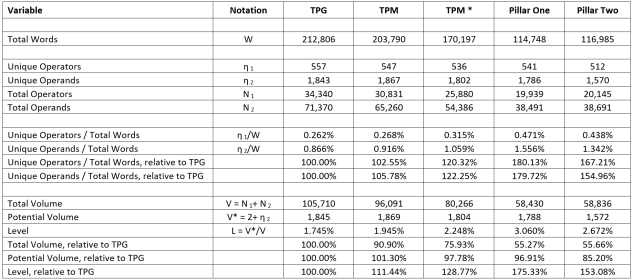
Our main results are reported in Table 2. We start with the overall word length of the four documents, which varies from a low of 114,748 (Pillar One) to a high of 212,806 (TPG); thus, the OECD Guidelines contain 85% more words than Pillar One. The total number of operands and operators, and the number of unique operands and operators, are also reported in Table 2.
Table 2: Operators, Operands, and Halstead Measures
Our first Halstead measure is the number of unique operators and operands in each document. The number of unique operators η1 is reasonably consistent across all four texts (about 540), with the score highest for TPG (557) and lowest for Pillar Two (512). The number of unique operands η2 is relatively close for the TPG, TPM, and Pillar One (about 1,800) with the TPM (with the country chapters) being the highest (1,867); Pillar Two has much lower diversity (1,570) in terms of unique operands. Given the wide breadth of topics covered by the TPG and TPM, and their greater word lengths, it is not surprising that they exhibit greater diversity of unique operators and operands than the blueprints.
In measuring rule complexity, Halstead also focused on the volume of the documents as measured by their actual volume (V = N1 + N2), potential volume (V* = 2 + η2), and Level (V*/V = (2 + η2) / (N1 + N2)). Our calculations show that the TPG has the highest volume (105,710) and Pillar One the lowest (58,430). The potential volume V* is highest for the TPM (1,869), closely followed by the TPG (1,845); V* is lowest for Pillar Two (1,572). Halstead’s level (L) metric, the ratio of potential to actual volume, varies from a low of 1.75% for the TPG to a high of 3.06% for Pillar One. The level for Pillar One is therefore 75% higher than for the TPG. Pillar Two also exhibits a higher level than the TPG (2.67%), which is 53% higher than the TPG. The TPM is also more complex, when measured by level, than the TPG (11% higher when the country chapters are included and 29% higher when they are excluded).
Having the word lengths for each of the documents suggests another way to capture rule complexity: the ratio of unique operands and operators as a share, respectively, of each document’s word length. In effect, this measure provides an estimate of the density of unique operands and operators in each document. Intuitively, the greater the density of the unique concepts and calculations, the greater the tax complexity of a document.
The number of unique operators as a percentage of total words (η1/W) in each document varies from a low of 0.262% for the TPG to a high of 0.47% for Pillar One; i.e., the density is 80% higher in Pillar One than in TPG. Pillar Two’s density is nearly as high (0.44%) as Pillar One’s; i.e., relative to the TPG, Pillar Two is 67% more dense in terms of unique operators. The same pattern is revealed for unique operands as a percentage of total words (η2/W), which varies from a low of 0.87% for the TPG to a high of 1.56% for Pillar One. In relative terms, this means that the density of unique operands is nearly 80% higher in Pillar One than in the TPG. Pillar Two’s density is nearly as high (1.34%); i.e., relative to the TPG, Pillar Two is 55% more dense in terms of unique operands. The UN Manual, conversely, is very close to the TPG in terms of density for both unique operators and operands, if the country chapters are included in the analysis. When the country chapters are removed, the density of unique operators and operands is 20% higher in the TPM than in the TPG.
Frequency
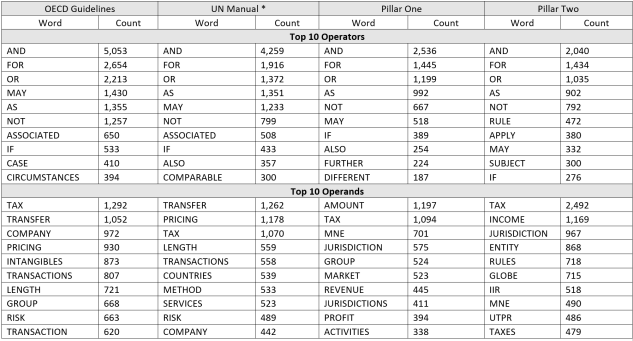
Looking at the ratio of unique operators and operands to word length of the documents suggests that examining their frequency could also be interesting. Table 3 lists the top 10 most frequently used operators and operands for all four texts. Note that the list of words and even their frequency ranks are quite similar across the texts (in particular, if one excludes Pillar Two), which confirms that the texts are roughly comparable in scope and purpose.
Table 3: Top 10 Operators and Operands by Word Count for Each Text
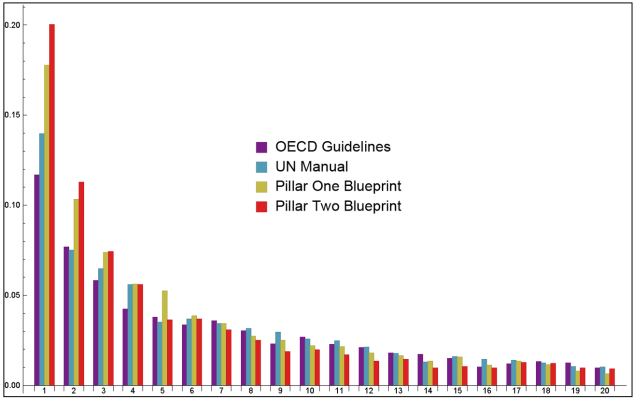
In Figure 2, we plot the frequency of all words in the four documents and find they are distributed quite differently. Namely, the Blueprints make use of many words that are used only once or twice in the entire text. For instance, 20% of the words in Pillar Two appear only once compared with 12% in the TPG. This means that either the Blueprints mention a wider variety of topics or that they use more synonyms to express the same ideas.
Figure 2: Histogram Showing Proportion of Words With Different Frequencies in Four Texts
Relative Rankings
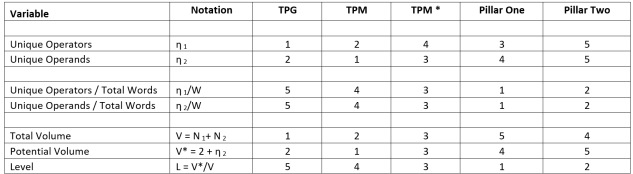
Our last table summarizes the relative rankings of the four transfer pricing documents on our different metrics for tax complexity, building on Halstead. The rankings in this table should be read with caution, given that differences in the raw scores underlying the rankings for a particular metric may be very small. In addition, we make no attempt to prioritize one measure over another. Assessments of overall tax complexity should consider all the metrics.
Table 4: Ranking of Documents by Tax Complexity Measure
To summarize our findings, first, the numbers of unique operands and operators are higher for TPG and TPM than for the Blueprints; TPG has the highest number of unique operators and TPM of unique operands. When adjusted for word length, we find that the Blueprints exhibit greater density of unique operands and operators than do TPG or TPM; that is, the Blueprints perform more unique operations and contain more unique operands for a given number of words. The ranking is consistent for both density metrics: Pillar One > Pillar Two > TPM > TPG. When the potential volume V* is compared to the total volume of operators and operands to generate level (L = V*/V), we find the same ranking, with Pillar One the highest and TPG the lowest level. In sum, while the Blueprints are individually much shorter documents than the TPG or TPM, our assessment is that the overall rule complexity in the two blueprints is greater in terms of the various Halstead metrics than either the TPG or the TPM.
The Economic Impact Assessment
For interest, we also assessed the tax complexity of the Economic Impact Assessment (EIA) released with the blueprints. The EIA is not truly comparable with the other texts because its focus was to determine the economic impacts of Pillars One and Two on interjurisdictional tax bases. We found that the tax complexity metrics for the EIA place it between the blueprints and the TPG and TPM. The EIA exhibits a greater density of unique operators (32%) and unique operands (33%) compared to the TPG and a level that is 41% higher than the TPG. See OECD/G20 Base Erosion and Profit Shifting Project, Tax Challenges Arising From Digitalisation—Economic Impact Assessment. Inclusive Framework on BEPS (Oct. 12, 2020). These results are available on request from the authors.
An Analogy: Making Soup
Perhaps it may be helpful to think of the various Halstead metrics using an every-day analogy. Consider a recipe for making a pot of soup. The cook needs a variety of ingredients and utensils of differing amounts and sizes specified in the recipe. The cook performs a variety of different operations using these ingredients and utensils, which take varying amounts of time.
Now conceptualize the recipe in terms of Halstead’s measures of rule complexity. A recipe is also a set of rules to follow. The mapping is direct: ingredients are operands. Anything that describes an action of the cook is an operator (“stir,” for instance). Cooking utensils are also operands (“stir with a spoon”), and function words are function words.
Our first Halstead measure of recipe complexity is the number of unique operators (e.g., chopping, stirring) and unique operands (e.g., vegetables, spices) involved in following the recipe. There is also some total number of steps (operations) to be performed and some total number of ingredients (operands) to be used. Our second measure is the share (or density) of the unique steps (operators) and unique ingredients (operands) in the overall making of the soup. The greater their density, the greater the complexity of the recipe. Our third measure is based on the minimum number of ingredients (operands) needed to make the soup. Halstead’s “level” measure computes the ratio of the minimum ingredient volume to the actual volume of ingredients and operations used in making the soup. Thus, the analogy is straightforward: The overall complexity of a recipe (or any regulatory document) depends on (i) the diversity of the unique ingredients and operations required to complete the task; (ii) their densities relative to the total task work involved; and (iii) the level of effort based on a comparison of the minimum number of ingredients with the total number of ingredients and operations in the recipe.
POLICY RECOMMENDATIONS
Our goal in this project has been to assess the tax complexity of the Pillar One and Pillar Two blueprints, by comparing them relative to the two major “status quo” international transfer pricing documents: the 2017 OECD Transfer Pricing Guidelines (TPG) and the 2017 UN Transfer Pricing Manual (TPM). We used a novel method for measuring tax complexity, which relies on interpreting tax rules as an algorithm. We found that both Blueprint documents appear to be more complex, in terms of our metrics, than either the TPG or TPM, with the Pillar One exhibiting the greatest complexity.
Some lessons emerge from our analysis that point to ways that tax authorities and international organizations can reduce the complexity inherent in their regulatory guidelines and manuals.
(1) The tax complexity of new rules should be compared to the complexity of existing comparable rules, with the goal of reducing the complexity of the new rules or at least ensuring that tax complexity is no higher than the status quo rules. Given that the blueprints exhibit significantly higher complexity than either of the existing status quo documents (the TPG and TPM), the OECD should focus its efforts on reducing tax complexity in subsequent iterations of these documents.
(2) A variety of tax complexity metrics should be calculated including (i) the number of unique operators and operands η1 and η2, (ii) the density of unique operators and operands relative to document length η1/W and η2/W, and (iii) the level of complexity as measured by the ratio of potential to total volume L = V*/V.
(3) Our tax complexity measure can be computed for each section of a legal text, or even for each paragraph. This would allow measuring which parts of the text are the most likely to increase complexity and where efforts at simplification should be focused. A similar effort could determine which sections of the Blueprints are most complex (comparing for instance the computation of Amount A and Amount B), which would suggest where efforts to simplify the document should be concentrated.
(4) The sections in the Blueprints could be checked to see which sections contribute the most to the very large number of operators in these two texts, and to ensure that this use of operators really corresponds to operations that are intended to be quite complex, or otherwise reduce their use where possible.
(5) Policy makers interested in reducing tax complexity could track words that are used once or a small number of times in the text. When a text has many such words, it can indicate the presence of many exceptions, qualifications, or other details that can greatly complexify the text beyond what is necessary. If keeping these details is necessary, a possibility is to split documents into a part for principles and a part for applications, where most exceptions would be moved to the application section. The OECD could also track the frequency of word usage in the blueprints with a goal of simplifying the text as much as possible; e.g., the “activity tests“ section (Pillar One, pages 22–61) might be a starting point.
(6) It is important to recognize that our paper has focused on one form of tax complexity. There are different components to tax complexity and attempts to assess and reduce the complexity of the documents (rule complexity) would still leave other forms of tax complexity intact.
CONCLUSIONS
Most taxpayers, tax authorities, and tax practitioners believe tax laws are too complex. International tax law is widely perceived to be even more complex and impose even higher compliance costs on taxpayers than domestic tax law. Reducing tax complexity has been a tax reform goal at the national and international levels for many years.
Our article is a first attempt to measure the rule complexity of the Pillar One and Pillar Two blueprints as compared to the “status quo” documents: the OECD Guidelines and the UN Manual. Applying our version of the Halstead complexity metrics to the four documents, we found that the rank ordering of complexity, across the metrics, can be summarized as: Pillar One > Pillar Two > TPM > TPG; that is, in general, Pillar One is the most complex and the TPG the least complex of the four documents. We also made some proposals for ways that the complexity of tax documents (whether regulations, guidelines, manuals or blueprints) can be reduced, together with specific suggestions for the blueprints.
Lessening the rule complexity of the Blueprints will not however, on its own, move the international tax system toward greater tax certainty. We agree with the assessment by Daniel Bunn (Tax Foundation), i.e., the Blueprints “fail to provide a clear and consistent vision for the international tax system.” Going back to basics—to broad and generally accepted tax principles—we argue is the best way to reduce tax complexity and ensure voluntary taxpayer compliance with international tax laws.
We also argue that layering another set of rules on top of the current international tax rules will create more tax complexity, not less. The Pillar One and Pillar Two proposals do not eliminate the need for the OECD Guidelines or the UN Manual. Instead, transfer pricing professionals, multinational enterprises, tax authorities, and tax courts would have to apply both the status quo rules and the Pillar One and Pillar Two proposals if adopted by members of the Inclusive Framework. Layering new rules on top of existing rules will inevitably make both sets of rules more complex. Our research suggests how much more complex the international tax rules could become if policy proposals in Pillar One and Pillar Two are adopted.
In fact, as David Kleist points out in his 2018 article in the Nordic Tax Journal assessing the tax complexity of the OECD Multilateral Convention to Implement Tax Treaty Related Measures to Prevent BEPS, the issue may actually be much worse than simply layering one set of rules on another. Kleist argues that the OECD’s Multilateral Instrument (MLI) exhibits substantial tax complexity and provides some reasons: (1) the MLI clauses are extensive, detailed, and technical; (2) an 85-page Explanatory Statement is needed to clarify the approach; (3) some rules stretch over multiple pages; and (4) the MLI’s flexibility allows for an “almost infinite number of combinations of reservations and options” (pp. 44-45). He concludes that reading and understanding the MLI is difficult for skilled tax professionals and likely “impenetrable” for laypersons. (Many of the points and criticisms that Kleist makes in his MLI assessment, we believe, also apply to the dispute prevention and resolution mechanisms in Chapter 9 of the Pillar One Blueprint.)
Moreover, Kleist also found that (1) not all countries had signed; (2) signing was not the same as implementing and there were different levels of implementation; (3) even those tax jurisdictions that did sign were permitted to sign onto some articles (which may still need implementing) and not others; and (4) only some articles have “teeth” (e.g., minimum standards) while most do not. If the blueprints were adopted—and as proposed they also have their own separate MLI—the same problems Kleist identified with the MLI are likely to reappear. Some countries will sign and others will not. Some will sign but not implement, or implement slowly and in idiosyncratic ways. Some articles will bind; others be flexible. And so on.
Lastly, complexity encourages searching for loopholes and opportunistic behaviors. Lorraine Eden in “Pillar One Tax Games” (Tax MGMT Int’l Journal, Dec. 31, 2020) outlines a variety of ways that Amount A in Pillar One offers opportunities for tax jurisdictions and multinationals to “game” the rules, increasing tax complexity. Amount A is only one of the proposals in the Blueprints for changing the existing international tax rules; we suspect the other proposals offer similar “tax game” opportunities.
Our research suggests that the Pillar One and Pillar Two Blueprints have raised—not lowered—the level of tax complexity facing MNEs, transfer pricing professionals, and tax authorities, and if adopted, could increase not only rule complexity but also other forms of tax complexity. Our measure of tax complexity therefore probably captures only the proverbial “tip of the iceberg.”
This column does not necessarily reflect the opinion of The Bureau of National Affairs, Inc. or its owners.
Author Information
Jean-Edouard Colliard is Associate Professor of Finance at HEC Paris and a co-holder of the HEC-Natixis-Polytechnique Research Chair in Analytics for Future Banking (colliard@hec.fr). Lorraine Eden is Professor Emerita of Management and Research Professor of Law at Texas A&M University (leden@tamu.edu). Co-Pierre Georg is Associate Professor at the University of Cape Town and holds the South African Reserve Bank Research Chair in Financial Stability Studies (co-pierre.georg@uct.ac.za). We thank Oliver Treidler, Martin Hearson, David Kleist, Michelle Markham, Ognian Stoichkov, and James Zhan, for helpful comments on an earlier draft. The views expressed in this report are solely the authors and do not reflect those of any other person or institution. Please address comments to Lorraine Eden at leden@tamu.edu. This article is a shortened version of the original article, which appeared in Tax Management International Journal on Feb. 5, 2021. A Bloomberg Tax login is required to access that article.
Bloomberg Tax Insights articles are written by experienced practitioners, academics, and policy experts discussing developments and current issues in taxation. To contribute, please contact us at TaxInsights@bloombergindustry.com.
To read more articles log in.
Learn more about a Bloomberg Tax subscription.